COVID-19感染リスク推定のためのAI・機械学習の基礎知識
目次
著者:佐藤能臣a,b,坂本唯史a,市原泰介b
所属:a(株)データフォーシーズ AI Lab
b日本システム技術(株)ライフイノベーション LAB
はじめに
中国・武漢が発生起源であると考えられているCOVID-19の世界規模の大流行は、世界の約2割でCOVID-19感染拡大リスクが今なお非常に高く[1]、流行が収束する兆しさえ見せていない(図1)。日本でも、新型コロナウイルスの変異株による感染拡大の第4波が地方に広がり、過去最多が15県にも上った[2]。Johns Hopkins University & Medicine, Coronavirus Resource Centerが公開するデータから[3][4]、現在までの世界と日本での感染者数・死亡者数・回復者数の累計は下の表1で示される。
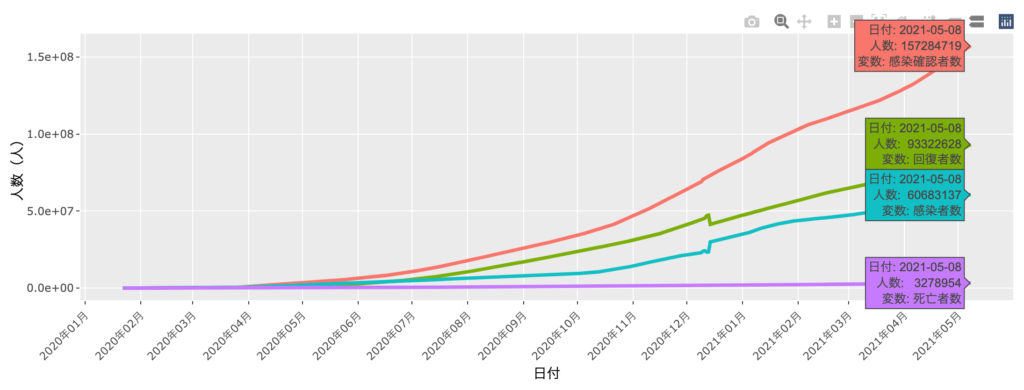 図 1 世界のCOVID-19感染状況(2021年5月8日時点)[1]
図 1 世界のCOVID-19感染状況(2021年5月8日時点)[1]
| 感染確認者数 | 回復者数 | 死亡者数 | |
| 世界 | 1億5768万人 | 9370万人 | 328万人 |
| 日本 | 64万人 | 55万人 | 1万人 |
表 1 世界と日本の感染状況の累計(2021年5月8日時点) [1]
COVID-19流行は、気象条件などの季節性にも影響されることが示唆されている[5]。特に、日本は、中国や韓国と隣接していたにも関わらず、1次感染拡大は、アジアの他の地域に比べ非常にゆっくりしていたが(図2。後で説明されるk-平均法による分類結果である。各国での感染拡大の時期の違いを見やすくするため、最大感染確認者数で正規化した)、梅雨という独特の気象条件の影響の可能性も重なり、4月中の自粛時期以上に感染が再拡大した。8月上旬から中旬にかけ感染者数ピークを迎え、現在は新規感染者数・感染者数は減少傾向を示している。しかし、社会的距離戦略などを踏まえた適切な拡大予防対策がなされなかったために、2021月1月の本格的な第3波、そして、現在の第4波と、第2波以上の感染拡大が起きてしまった。
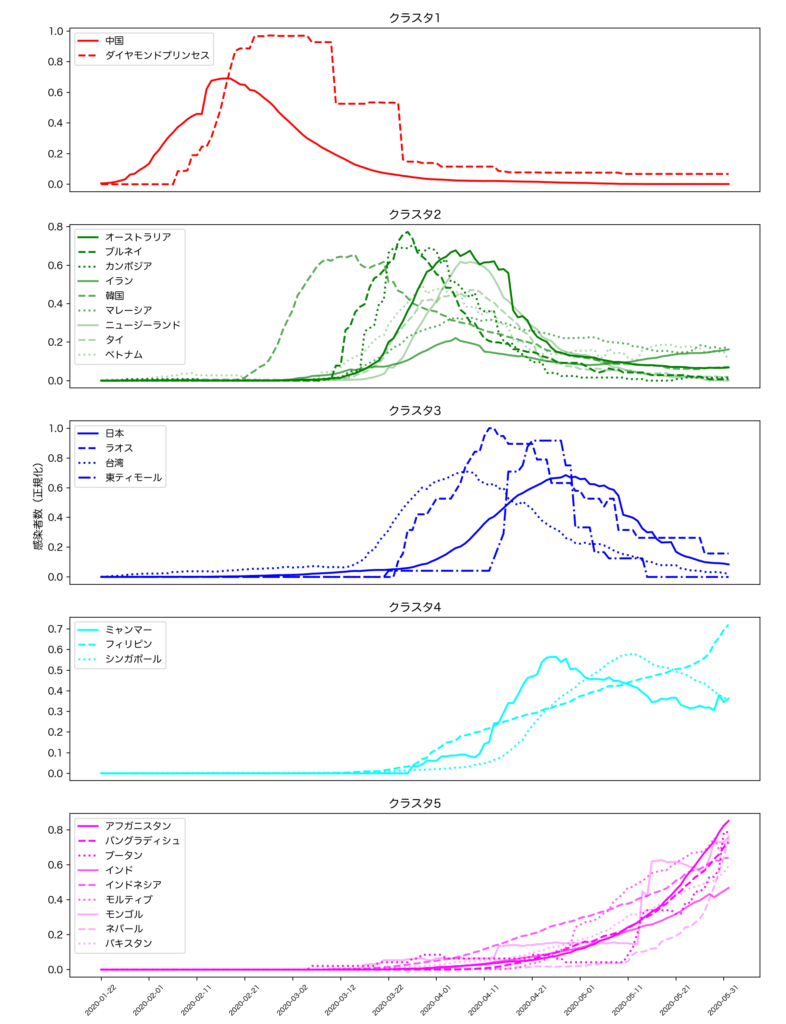 図 2 k-平均法によるクラスタ1-5のCOVID-19感染推移
図 2 k-平均法によるクラスタ1-5のCOVID-19感染推移
本稿では、国民の感染危機や感染予防の意識向上や、経営改善に関する適切な施策の提案を目指し、累積統計の可視化に止まらず、統計・AI・機械学習の基礎から透明性の高い科学的根拠を持って、一般の人々に分かりやすく感染リスクの定量化を説明する。
AI・機械学習
データセット
2021年4月28日に正式に公開された「JAST-D4c 新型コロナウイルス感染症(COVID-19)感染リスク分析ダッシュボード」[2]で用いられるCOVID-19感染状況データは、世界各国の感染情報に関するデータは、Johns Hopkins University & Medicine, Coronavirus Resource Centerが公開するサイト[3][4]から取得する。一方、国内のCOVID-19感染状況に関するデータは、ジャッグジャパン(株)[6]や「COVID-19 Japan 新型コロナウイルス対策ダッシュボード」[7]が提供するデータを利用している。また、日本を含む世界各国のワクチン接種状況に関するデータは、Our Data in Worldの「Coronavirus (COVID-19) Vaccination」から取得する[8]。
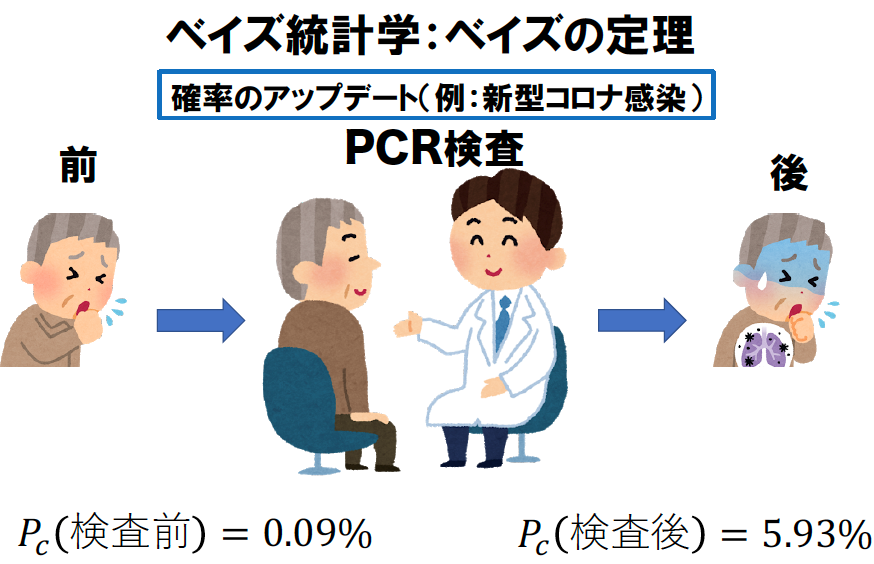 |
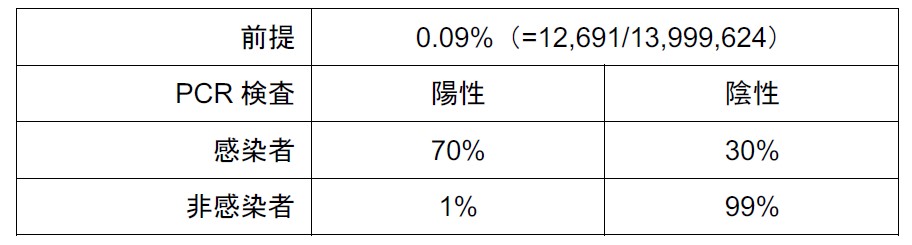 表 2 東京都2020年8月1日のPCR検査集団の指標[14] 表 2 東京都2020年8月1日のPCR検査集団の指標[14]
|
ベイズ統計
ベイズ統計は、トーマス・ベイズ[9][10]によって提案されたベイズの定理が基盤となり、1700年代に確立された理論である。ベイズの定理により、人々が持つ先験的な確信(原因:例えば,専門家の意見に基づいたりして獲得される事前の情報)を観測データ(結果)と結び付けることで、推定される確率(逆確率)を求めることができるので[11]、しばしば、「確率の更新(アップデート)」として指すこともあり、その応用範囲は、診断検査[12][13]から時系列予測[14]に至るまで非常に幅広い。東京都の2020年8月1日の新型コロナPCR検査集団の指標(図3)[15]と2020年7月時の東京都の新型コロナ感染率(表2の前提)から、この「確率の更新」を新型コロナの感染率から考えてみよう。2020年7月の東京都の新型コロナ感染率を

とする。ここで分母を「東京都の人口(推計)–過去の推計–」[16]の2020年7月時点の東京都の総数(推計)とし、分子を「COVID-19 Japan -新型コロナウイルス対策ダッシュボード-」[7]の2020年7月時点の東京都の累計感染確認者数とした。
図3で示されるように、新型コロナPCR検査を受けて陽性と診断されてしまった時の新型コロナに感染した確率Pc(検査後)は、次のように推定することができる:
- 検査前の前提だった新型コロナの感染率を事前確率とする。
- 新型コロナ感染が「原因」となって、陽性と判定される「結果」に関する条件付確率は、テーブルの70%である。
- 検査での陽性判定が「原因」となって肺炎を罹患した「結果」となる同時確率は
P(感染∩陽性)=P(陽性|感染)P(感染)
より
0.7×0.0009=0.00063
となる。新型コロナに感染しなかった場合の非感染率は、
事前確率=1-0.0009=0.9991
となる。
新型コロナに感染しなかったが「原因」となって、陽性と判定される「結果」の条件付確率は,テーブルの1%である。
検査での陽性判定が「原因」となって、新型コロナに感染しなかった「結果」となる同時確率は、
0.01×0.9991=0.009991
となる。検査で陽性判定を受け、新型コロナに感染してしまった率は、
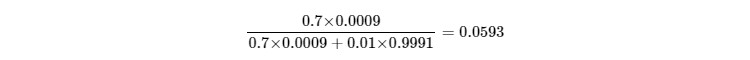
で、5.93%となると考えられる。
これは、検査前の新型コロナ感染率が、上の表のPCR検査(新型コロナの感染が「原因」で陽性判定を受けた「結果」の条件付確率)を通して、約65.9倍に更新されることを意味する。より正確には、「2020年8月1日時点でのPCR検査の精度では、2020年8月以降の東京都の新型コロナの感染率は、5.93%、即ち、『約100人に6人が新型コロナに感染する』可能性がある」ことを示唆するものである。実際、第4波の拡大中の2021年4月30日時で、東京都の感染率は、約1%、即ち、約100人に1人が新型コロナに感染している。 ベイズの定理は、新型コロナの感染や1つの疾患の罹患だけでなく、複数の疾患を想定する場合や、複数の疾患を複数の診断法で診断する場合にも適用することも可能である[12]。また、ベイズの定理を用い、中国における感染拡大時でのCOVID-19感染検査の信頼性を評価した研究報告もなされている[17]。前述のように、過去の疾病の罹患率などの事前に獲得された情報をCOVID-19感染状況の観測データと結び付けることで、感染リスクをCOVID-19との合併による重症化のリスクの定量化も可能であると考えられる。
k-平均法
k-平均法[18][19]とは、ラベル情報のないデータを分類する手法(教師無し学習の一種のクラスタリング)の1つであり、そのゴールは、以下の関数値(データ間の距離)が最も低くなるように、各データがK個のグループ()(C1,…,Ck)のうちのどのグループに属するかを決める手法である:
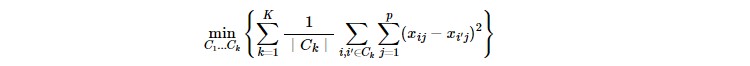
このk-平均法を用い、世界各国のCOVID-19感染状況に関する時系列に潜むデータ構造を見出す。図2は、2020年1月22日から2020年6月1日までのクラスタ数がk=5の時の東アジアから南アジアにかけての第1次感染拡大の推移を可視化した結果である。図2が示すように、各クラスタが任意の拡大期間で分類されるように、その平均からの距離を最小にしているがわかる。このクラスタ分析により、日本が中国と隣接しているにも関わらず、台湾や韓国、東南アジア諸国に比べ、第1次感染拡大が非常に遅いことを示したことは、大変興味深い結果である。
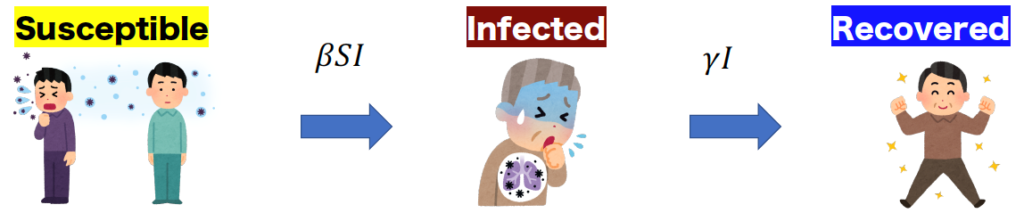 図 4 感染症SIRモデルの概念図
図 4 感染症SIRモデルの概念図
感染症数理モデル
COVID-19がどのように感染拡大するか、その時の感染者数、或いは、流行の期間などを予測したり、基本再生産数(疫学的には、感染症への感受性をもつ全個体の集団を仮定し、1感染個体から直接生み出される感染個体数の平均と考えられ、集団内の感染症の蔓延する速度を推定するものではないことに注意する)などの様々な疫学的パラメータを推定したりするためには、また、異なる公衆衛生上の介入が流行の結果にどのような影響を与えるかを示すためには、数理モデルを用いることが非常に有効であると考えられている。代表的な感染症数理モデルの1つとして、1927年にW.O. KermackとA.G. McKendrickによって提案されたSIRモデルが挙げられる[20]。このSIRモデルから推定される基本再生産数R0は,R0>1が感染症の集団内で蔓延を表し、その値が大きいほど流行を抑えることが難しく、R0<1は、感染症が蔓延しないことを表す。ここでは、Johns Hopkins University & Medicine, Coronavirus Resource Centerが公開するサイト[3][4]から取得されるCOVID-19時系列データをSIRモデルに当てはめられると仮定し、[21][22]を参考に、相図分析による感染拡大・収束の推定方法を説明する。SIRモデルは,次のように記述される:
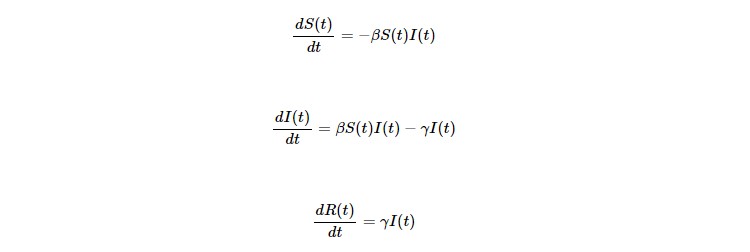
このとき、S(t)、I(t)、R(t)は、それぞれ、感受性保持者数、感染者数、回復者数を表す。また、上式の、β、γは、それぞれ感染率、回復率である。上式の時間発展方程式は、以下の仮説に基づいて成り立つものとする:全人口は、感受性保持者(Susceptible)、感染者(Infected)、回復者(Recovered)の3つ分けられるものとする。そして、感受性保持者数は、感受性保持者数と感染者数の積に比例した感染率(βS(t)I(t))で感染者に移行し、感染者は、指数分布に従った感染期間に基づき、回復率との積(γI(t))で回復者に移行するものとする(図4)
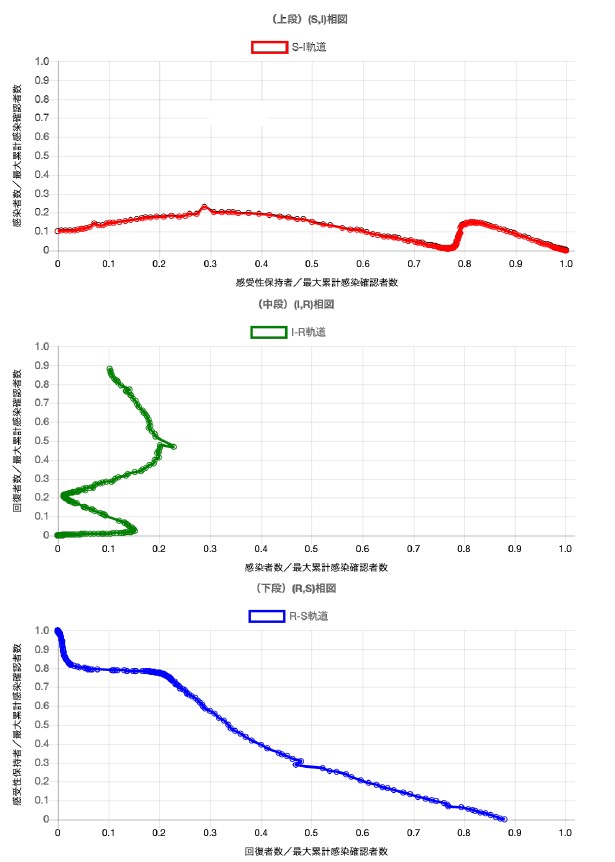 図 5 (S,I,R)相図
図 5 (S,I,R)相図
また、感染率と回復率の2つパラメータを用い、基本再生産数は、
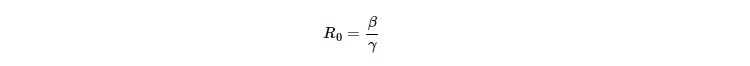
として表される。COVID-19感染状況では、S(t)が未知であるが、感染が一旦収束した時期の感染確認者の累計(ほぼ一定値をとる)を総人口と仮定し、
![]()
とする。図5の上段の(S,I)相図の軌道分析をする。初期値を(S(0),I(0))=(1,0)とすると、S(t)の減少とともにI(t)が増加し、ピーク後急速に減少していく軌道を描く。2次感染拡大がなければ、本来は、S(∞)=I(∞)=0の終息軌道を描くだろう。そのような軌道上のピーク、即ちdI/dS=0、(即ち、dI/dt=0)となる変曲点(Sm,Im)から基本再生産数Rmが求められる:
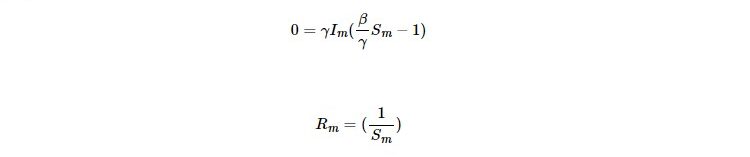
実際の総人口は、ほぼ一定値をとる累積感染確認者数よりも多いので、基本再生産数は、R0≲Rmとなると考えられる。しかし、2020年のCOVID-19大流行は、夏に2次感染拡大が起きてしまい、2020年から2021年にかけては第3波も起こった。図5の中段の(I,R)相図や下段の(R,S)相図を含む3次元(S,I,R)相図から、日本のCOVID-19流行は、将来、(S(∞),I(∞),R(∞))=(0,0,1)となるような収束軌道を描くことが予想される。(S,I,R)の3変数は、感染収束の特徴量として、収束状態からの距離(恐らく,マハラノビス距離に相当)から収束確率を算出できるかもしれない。
謝辞
本論文の結果の一部は、日本システム技術(株)ライフイノベーションラボとの共同研究開発のもとで行われた。議論や意見を頂いた(公財)佐々木研究所附属杏雲堂病院の相馬正義院長に心から感謝します。
参考文献
[1] 「JAST-D4c 新型コロナウイルス感染症(COVID-19)感染リスク分析Dashboard」日本システム技術株式会社 イノベーション Lab & データフォーシーズ AI Lab (https://the-jast-d4c-risk.shinyapps.io/main/ 2021年4月28日)
[2] 毎日新聞「15道県で感染最多、地方拡大鮮明 全国で新たに7247人感染」(https://mainichi.jp/articles/20210508/k00/00m/040/218000c 2021年5月8日)
[3] 「COVID-19 Dashboard (COVID-19 Map)」Johns Hopkins University & Medicine, Coronavirus Resource Center https://coronavirus.jhu.edu/map.html (2020).
[4] https://github.com/CSSEGISandData/COVID-19
[5] Mohammad M Sajadi, et al. “Temperature, Humidity, and Latitude Analysis to Estimate Potential Spread and Seasonality of Coronavirus Disease 2019 (COVID-19).” JAMA Netw Open. 2020; 3:e2011834.
[6] 都道府県別新型コロナウイルス感染者数マップ(ジャッグジャパン株式会社提供)- Dashboard&Map of COVID-19 Japan Cas
[7] COVID-19 Japan -新型コロナウイルス対策ダッシュボード- https://stopcovid19.jp (2020年3月18日)
[8] 「Coronavirus (COVID-19) Vaccinations」 Our World in Data, https://ourworldindata.org/covid-vaccinations, https://github.com/owid/covid-19-data/tree/master/public/data/vaccinations
[9] https://en.wikipedia.org/wiki/Thomas_Bayes
[10] C. M. ビショップ(著)元田浩等(訳)「パターン認識と機械学習 上 – ベイズ理論による統計的予測」(丸善,2007)
[11] J. P. Klein, M. L. Moeschberger(著)打破守(訳)「Survival Analysis-2nd Edition 生存時間解析」(丸善出版,2012年)
[12] 森實敏夫(著)「新版 入門 医療統計学-Evidenceを見出すために」(東京図書,2016年)
[13] 折笠秀樹「ベイズ統計の応用領域 としての診断検査」 Jpn. Pharmacol. Ther. (薬理 と治療) vol.47 no.8, (2019)
[14] S.Kozawa, T.Akanuma, T.Sato, Y.D.Sato, K.Ikeda, T.N.Sato “Real-time prediction of cell division timing in developing zebrafish embryo” Scientific Reports Vol. 6, 32962, (2016)
[15] 上田耕蔵「新型コロナ Q&A その27」日本災害看護学会 (http://www.jsdn.gr.jp/CMS/wp-content/uploads/8346032501facebb0f91f4dcff2365c2.pdf)
[16] 東京都の統計「東京都の人口(推計)–過去の推計–」(https://www.toukei.metro.tokyo.lg.jp/jsuikei/js-index2.htm)
[17] A. Chen “Bayes’ Rule, Unreliable Diagnostic Testing, And Containing COVID-19” towards data science Sharing concepts, ideas and codes (February 16th 2020)
[18] H. Steinhaus “Sur la division des corps matériels en parties” (French). Bull. Acad. Polon. Sci. 4 (12): 801–804 (1957).
[19] 久野遼平・木脇太一「[図解]大学4年間のデータサイエンスが10時間でざっと学べる」(KADOKAWA,2018年3月24日)
[20] W. O. Kermack and A. G. McKendrick “A Contribution to the Mathematical Theory of Epidemics”. Proc. Roy. Soc. of London. Series A 115 (772): 700-721 (1927). doi:10.1098/rspa.1927.0118. JFM 53.0517.01
[21] Malaria Math “Phase Plane Analysis of Kermack-McKendrick Model.” (2017)
[22] M. Martcheva “An Introduction to Mathematical Epidemiology.” (Springer, 2010).





